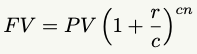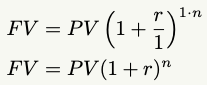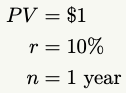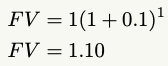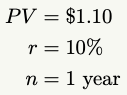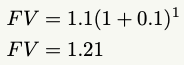Finding the Future Value of Money
I read everything about land and real estate-backed notes that’s out there, so I was looking forward to reading Invest Like a Bank by Beaux Blast. Particularly since it’s rated 4.6 out of 5, with hundreds of positive reviews.
Disclaimer: This post is a bit math-heavy.
However, in reading the section on future value I grew suspicious. Here’s what the author wrote:
Note investing is made up of 2 basic concepts. The first is the future value of money: how much will your dollar be worth at some point in the future. Fortunately, this concept can be stated as an equation: (1+1)ᴺ.
That’s certainly not the formula for future value. Nevertheless, the author reassures the reader they shouldn’t worry if they’re scared of math, he’ll explain everything. He then gives some examples:
Take $1 and compound it by 10% over some time.
(1+1)¹⁰ = 1.10
Aside from being a nonsensical equation, the resultant answer is actually $1,204. Blindly charging ahead, the book continues with a follow-on example:
After 1 year, your dollar would be worth $1.10. What will it be worth after 2 years?
(1.1 + 1)¹⁰ = 1.21
Your dollar would be worth $1.21 because we are performing the calculation on the new value of $1.10.
This equation purports to equal $1.21, when in fact it equals $1,667.98.
Let’s turn away from the author’s fundamental misunderstanding of future value and focus on a true grasp of the concept.
Here’s the equation to calculate the future value of compound interest:
With the following:
If we’re compounding a single time each year, as it appears the author was attempting, we can simplify the equation further:
Meaning, when compounding once a year, we’ll only need to focus on the following variables:
Returning to the examples given in the book, let’s calculate it properly. If we’re taking $1 and compounding it by 10% over 1 year, we’ll solve for FV with the following variables:
Entering this into the future value equation we find:
So after 1 year, we’ve shown a dollar will be worth $1.10. To follow the author’s second example, we can determine the value after the second year, given what we know following the first year.
To do so, we’ll use the following variables:
To find the resulting answer of:
Or more simply, to accomplish this from the onset we’d use the following variables:
To also arrive at the correct answer:
As a brief aside, I attempted to reach out to the author with a friendly message so he could correct the manuscript and better serve future readers — particularly novices who would be misdirected.
As it turns out, their name isn’t connected to anyone real and their “photo” was taken from a free website. It’s simultaneously used by hundreds of other websites around the world.
Certainly lends credence to the adage “don't believe everything you read."
Even if it has 4.6 stars.